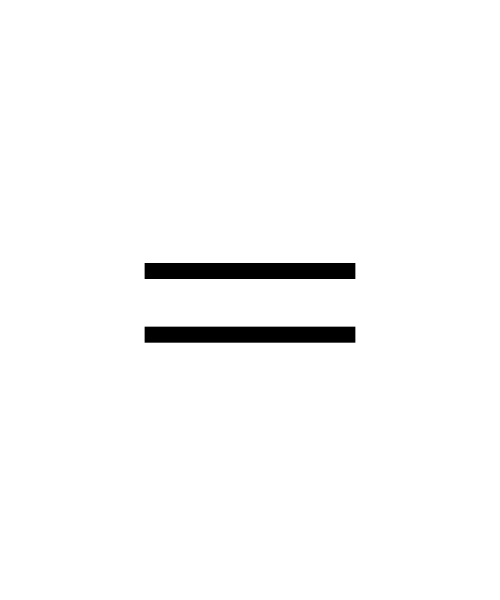I've been scratching my head, rather anxious about our prospects of success. Our algebra 2 course is essentially a class about the major functions of mathematics - polynomial, rational, radical, logarithmic, exponential, and trigonometric. For each unit, we do the same set of things - graph, solve, and model.
After working with them for a couple of weeks, I developed a suspicion that they don't really understand what we're working with - specifically, the equals sign. They can somewhat reliably graph and solve basic equations, but I've seen little evidence that they understand what these actually represent.
So, I took five minutes from class yesterday and had them answer a few questions. Here are the questions with some typical responses:
- What is an equation?
- A problem that can be solved mathematically.
- Something that has an end solution through multiple applications.
- A problem you solve to get an answer.
- It is a sequence of #'s and variables, and your job is to find the right answer to it.
- Numbers or letters used to represent or solve something.
- What is a graph?
- A grid where you plot points.
- A typically square thing you draw a line on.
- Where points are plotted and to show increase and decrease.
- A graph is a visual equation.
- A graph is like another way of showing your work when you solve an equation.
While there are some glimmers of hope in there, I think this is going to be a barrier for us. Students will not be able to reach the depth of understanding that I desire unless they understand what that damn equals sign actually means. And I think this boils down to looking at operators, relations, variables, constants, and expressions. Maybe not using that language, but building on those ideas.
So, here's my plan. I'm going to students do an open sort with the following:
- Relations: =, <, >, ≤, ≥
- Operators: +, -, ÷, ×
- Variables: x, y, z
- Constants: 0, 1, 2, 3
- Expressions: 3x + 4, 5 - 1, 4ab
- Equations/inequalities: 2x ÷ 5 = 4, 2 - y < x, 5a ≥ 8b, 1 + 1 = 2
After the items have been sorted, I'll encourage student to create a hierarchy of their groups. I really want to focus on the groupings - what do things have in common, how are they different, and what do they represent.
In the end, I'm hoping that my students have a better understanding of equality as a relationship, and that an equation is simply a statement that two expressions have the same value.
I would really appreciate any feedback before I give this a go!